Algorithme

---

Algorithmique et Programmation

 

But de l’enseignement

Obtenir de la «machine» qu’elle effectue un travail à notre place

Problème: expliquer à la «machine» comment elle doit s'y prendre

Mais... comment le lui dire ou le lui apprendre afin qu’il fasse le travail aussi bien que nous, voir mieux que nous?

Objectifs

• • Résoudre des problèmes «comme» une machine
  • Savoir expliciter son raisonnement
  • Savoir formaliser son raisonnement
  •   Concevoir et écrire des algorithmes (séquence d’instructions qui décrit comment résoudre un problème particulier)
  • Selon le Petit Robert : "ensemble des règles opératoires propres à un calcul.”
  • Un peu plus précisément : Une séquence de pas de calcul qui prend un ensemble de valeurs comme entrée et produit un ensemble de valeurs comme sortie.
  • Un algorithme résout toujours un problème de calcul. L’énoncé du problème spécifie la relation E/S souhaitée.
  • Un algorithme, traduit dans un langage compréhensible par l’ordinateur (ou langage de programmation, ici le C), donne un programme, qui peut ensuite être exécuté, pour effectuer le traitement souhaité

 

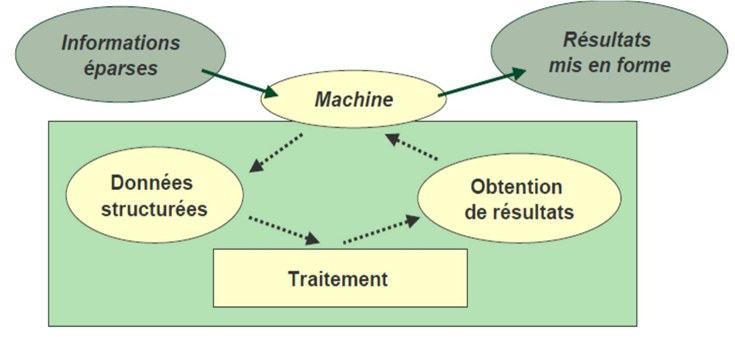
Savoir expliquer comment faire un travail sans la moindre ambiguïté

• • Langage simple : des instructions séquentielle
  • Suite   finie   d'actions    à    entreprendre     en    respectant une chronologie imposée

 

Un algorithme est indépendant de

• • Le langage dans lequel il est implanté,
  • La machine qui exécutera le programme correspondant.

Structure d’un algorithme

Un algorithme doit être lisible et compréhensible par plusieurs personnes.

Algorithme : Nom d’Algorithme Données : Les entrées de l’algorithme Résultats : Les sorties de l’algorithme Déclarations : Variables, constantes… Début

Ensemble d’instructions ;

Fin

Les étapes d’un algorithme

• Préparation du traitement
  • Données nécessaires à la résolution du problème
• Traitement
  • Résolution pas à pas, après décomposition en sous-problèmes si nécessaire
• Edition des résultats
  • impression à l’écran, dans un fichier, etc.

Exemple :

Variables Nombre, Inverse: entiers {déclarations: réservation
d'espace-mémoire}
Début
{préparation du traitement} Ecrire("Quel nombre voulez-vous élever au carré?") Lire(Nombre)
 

Inverse ←1 / Nombre
 
{traitement : calcul de l’inverse}

{présentation du résultat}
 
Ecrire("L’inverse de ", Nombre,"c'est ", Inverse)
fin.

Les problèmes fondamentaux

• Complexité
  • En combien de temps un algorithme va -t-il atteindre le résultat escompté?
  • De quel espace a-t-il besoin?
• Calculabilité
  • Existe-t-il des tâches pour lesquelles il n'existe aucun algorithme ?
  • Etant donnée une tâche, peut-on dire s'il existe un algorithme qui la résolve ?
• Correction

Peut-on être sûr qu'un algorithme réponde au problème pour lequel il a été conçu?

Logique propositionnelle :

La logique : une façon de formaliser notre raisonnement

La logique propositionnelle: modèle mathématique qui nous permet de raisonner sur la nature vraie ou fausse des expressions logiques

Proposition: expression qui peut prendre la valeur VRAI ou FAUX

Exemple :

 x > y 1+1=2

1+1=1

Eléments de logique propositionnelle

• Formule : expression logique composée de variables propositionnelles et de connecteurs logiques
• Variable propositionnelle : une proposition considérée comme indécomposable
• Connecteurs logiques: négation non ,¬ ; implication ⇒ ; disjonction

ou, 𝗏 ; conjonction et , 𝖠

Exemple : p et q variables propositionnelles

 

Tables de vérité

Représentation des valeurs de vérité associées à une expression logique

p et q : variables propositionnelles

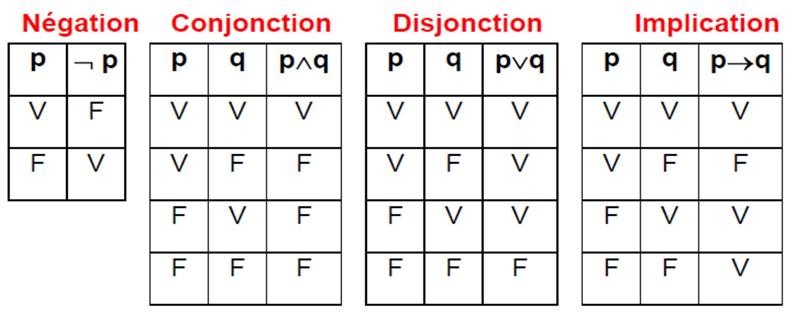
Equivalences classiques

• Commutativité
  • p 𝖠q équivalent à q 𝖠p
  • p 𝗏q équivalent à q 𝗏p
• Associativité
  • p 𝖠(q𝖠r) équivalent à (p 𝖠q) 𝖠r
  • p 𝗏(q 𝗏r) équivalent à (p 𝗏q) 𝗏r
• Distributivité
  • p 𝖠(q 𝗏r) équivalent à (p 𝖠q)𝗏(p𝖠r)
  • p 𝗏(q 𝖠r) équivalent à (p 𝗏q)𝖠(p𝗏r)

Lois de Morgan

¬(p 𝖠q) équivalent à (¬p) 𝗏(¬q)

¬(p 𝗏q) équivalent à (¬p) 𝖠(¬q)

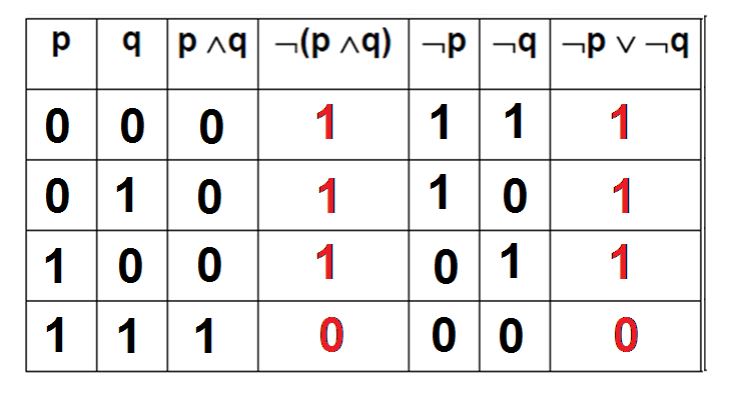
Formules

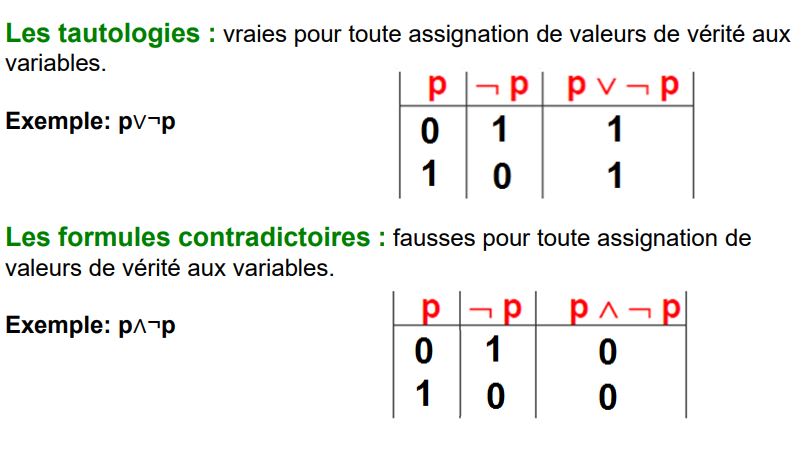
Applications à l'algorithmique

Interpréter(et bien comprendre!) l’arrêt des itérations à la sortie d’une boucle.

tant que<condition> faire

À la sortie :non(<condition>)est vrai

donc si condition= p et q À la sortie : non(p et q)

c’est a dire non p ou non q

Exemple:

avec <condition> égal à: val ≠STOP et nbVal< MAX

non(<condition>) égal à: val =STOP ounbVal≥MAX

Applications à l'algorithmique

• Simplifier une écriture par substitution d'une formule équivalente

si (Age = "Mineur"

ou (non (Age = "Mineur") et non (Fisc = "Imposable"))) alors...

Equivalent à :

si (Age = "Mineur" ou non (Fisc = "Imposable")) alors...

Vérifier la validité d'une condition

si Valeur< 10 et Valeur >100 alors… cas improbable

Ecrire la négation d’une condition

si on veut P et Q et R :

répéter …. tant que nonP ou nonQ ou nonR ou…