On utilise les " systèmes de numération" pour compter des objets et de les représenter par des nombres.
Trois notions interviennent dans un système:
Dans la base 10 "système décimal ", il y a dix digits: 0,1,2,3,4,5,6,7,8 et 9 appelés
(1234)10= 4x100 + 3x101 + 2x102 + 1x103 = 4 + 30 + 200 + 1000
Dans ce système, la base B vaut 2, et il y a donc 2 digits 0 et 1 appelés dans ce cas " BIT" (Binary digIT).
Par exemple, le nombre 1011 exprimé en binaire signifie:
(1011)2 = 1x20 + 1x21 + 0x22 + 1x23
=1 + 2 + 8
=(11)10
Dans ce système, la base vaut 8 et il y a 8 digits: 0,1,2,3,4,5,6 et 7. Il n'y a pas de chiffres 8 et 9.
Par exemple: le nombre 275 exprimé en octal:
(275)8 = 5x80 + 7x81 + 2x82
= 5 + 56 + 128
= (189)10
Dans ce système, la base B vaut 16 et il y a 16 digits: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E et F. Les dix premiers digits de 0 à 9 sont les chiffres du système décimal et les digits de 10 à 15 sont les premières lettres majuscules de l'alphabet.
Exemple, le nombre BAC exprimé en hexadécimal :
(BAC)16 = Cx160 + Ax161 + Bx162
=12 + 10x16 +11x256
=12 + 160 + 2816
=(2988)10
(3F9)16 =9x160 + 15x161 + 3x162
=9 + 240 + 768
=1017
On peut remarquer que 8 = 23;
On peut donc faire correspondre à chaque digit d'un nombre exprimé en octal un ensemble de 3 bits du même nombre exprimé en binaire. Par exemple:
(763)8 = (111)(110)(011)
=(111110011)2
La conversion inverse, binaire → octal, se fait de la même façon, en décomposant le nombre binaire par ensembles de 3 bits à partir de la droite.
Par exemple: (10111011101) 2=(2735)8
De la même manière, on peut remarquer que 16=24
On fera donc correspondre à chaque digit d'un nombre hexadécimal 4 bits du nombre binaire correspondant.
Par exemple : (A28)16=(101000101000)2
La conversion inverse, binaire hexadécimal, se fait en décomposant le nombre binaire par ensembles de 4 bits à partir de la droite.
Par exemple:
(101110011101001)2 = ( 0101)(1100)(1110)(1001) = (5CE9)16
L'expression hexadécimal d'un nombre binaire est très utilisée pour interpréter des résultats fournis par un "microprocesseur".
La conversion de l'expression décimale d'un nombre en son expression binaire, octale ou hexadécimale repose sur la recherche des multiples des puissances successives de la base (2,8 ou 16 selon le cas) que contient ce nombre. La méthode pratique consiste à effectuer des divisions successives: du nombre par la base, puis du quotient obtenu par la base, puis du nouveau quotient par la base,… jusqu'à ce que le quotient devienne nul. L'expression cherchée est constituée par l'ensemble des restes successifs des divisions, lu à l'envers.
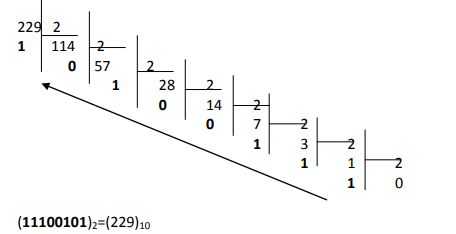
la même méthode serait applicable pour les conversions :
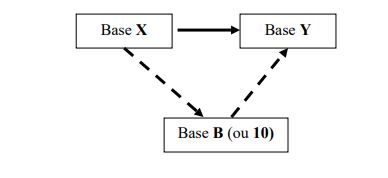
si X = Bm et Y= Bn
Alors convertir le nombre de la base X (Bm ) vers B puis de la base B vers la base Y (Bn )
Sinon Convertir de la base X vers la base 10 puis de la base 10 vers la base Y
