Codes Numériques
CODAGE
On distingue deux catégories de codes: les "codes numériques" qui permettent seulement le codage des nombres, et les "codes alphanumériques" qui permettent le codage d'une information quelconque (ensembles de lettres, de chiffres et de symboles).
Codes numériques
Le code binaire naturel est le code dans lequel on exprime un nombre selon le système de numération binaire.
Quelques notions:
-
- un quartet : c'est un mot de 4 bits (0-15)
- un octet : c'est un mot de 8 bits (0-255)
- un "kilo" : unité de capacité de traitement numérique (10 bits: 0-1023)
Inconvénients du code binaire naturel:
-
- nécessite une grande quantité de bits pour exprimer un nombre
- peut introduire des erreurs lors du codage de grandeurs variant de façon ordonnée. Entre deux codes successifs, plusieurs bits pourront alors être amenés à changer simultanément:
01 → 10 (01 →11→ 10 ou 01→ 00→ 10)
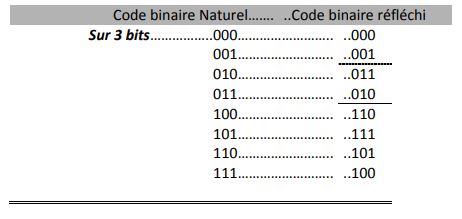
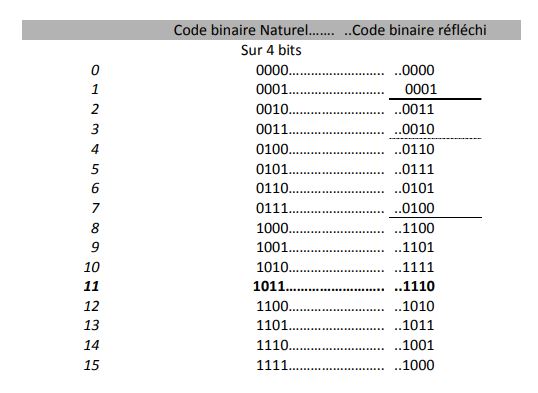
Dans ce code, appelé code GRAY, un seul bit change de valeur entre deux codages successifs. Il est construit de proche en proche, de telle sorte que chaque fois que l'on ajoute au code un bit sur sa gauche, on recopie au dessous de combinaisons existantes les mêmes combinaisons, mais en les écrivant dans l'ordre opposé.
Méthode
La valeur numérique d'un nombre binaire réfléchi s'obtient en donnant aux chiffres successifs pris de droite à gauche les poids 1,3,7,15,…2n+1 –1 et en effectuant la somme des produits non nuls, de signes alternés.
Exemple:
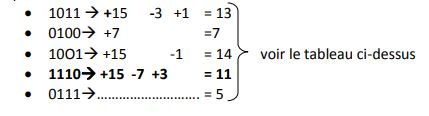
Autre méthode:
Pour trouver l'expression d'un nombre binaire dans le code réfléchi, on l'additionne sans effectuer la retenue, avec le nombre obtenu en le décalant vers la gauche d'un rang et on abandonne le chiffre du plus petit poids.
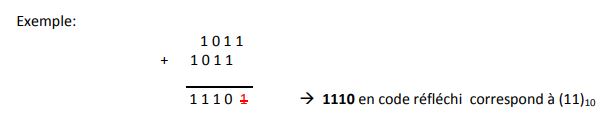
On code chaque chiffre (0-9) en binaire sur 4 bits ( 23 < 10≤24). Ce code est appelé DCB: (Décimal Codé en Binaire) en anglais BCD: Binary Coded Decimal
(1297)10 = (0001 0010 1001 0111)BCD
Question :comment représenter un nombre négatif en représentation binaire?
-
- arithmétique binaire

A+C+1 = 2n, or on travaille sur n bits, et 2n est représenté par n zéro, on a alors une représentation unique de 0.
B= 2n – A est appelé le complément à 2 du nombre A. A +B s'écrit 0 sur n bits.
B=2n –A =C+1
Conclusion:
Pour avoir la représentation d'un nombre négatif en complément à 2, on complémente tous les bits et on ajoute 1
Exemple: code binaire signé sur 4 bits.

Rappel:
Soit une base b associée à b symboles {S0, S1, S2, ..., Sb-1}
Un nombre positif N dans un système de base b s’écrit sous la forme polynomiale:
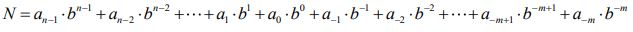

Méthode:
On multiplie la partie fractionnaire par la base en répétant l'opération sur la partie fractionnaire du produit jusqu'a ce qu'elle soit nulle (ou que la précision voulue soit atteinte).
Pour la partie entière, on procède par divisions comme pour un entier.
Exemple :
conversion de (54,25)10 en base 2 Partie entière : (54)10 = (110110)2 par divisions.
Partie fractionnaire :
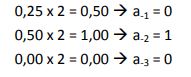
(54,25)10= (110110,01)2

NB: Une longueur finie en base 10 peut être infinie en base B On conserve la précision relative 10-3 est approximée par 2-10
Le codage en complément à deux sur n bits ne permet de représenter qu'un intervalle de 2n valeurs. Pour un grand nombre d'applications, cet intervalle de valeurs est trop restreint. La représentation à virgule flottante (floating-point) a été introduite pour répondre à ce besoin.
Pour des mots de 32 bits,:
- la représentation en complément à deux permet de coder un intervalle de 232 valeurs
- tandis que la représentation à virgule flottante permet de coder un intervalle d'environ 2255 valeurs.
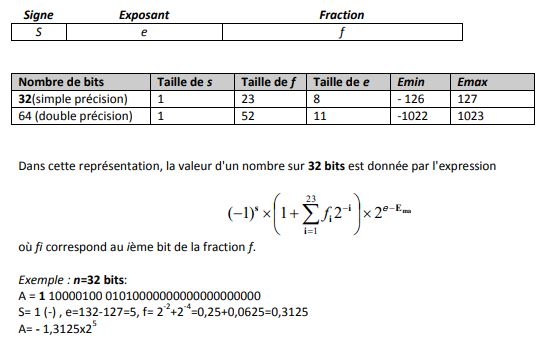
La représentation en virgule flottante a été normalisée (norme IEEE 754
Figure 1. Représentation des nombres à virgule flottante dans la norme IEEE 754
Pas encore de commentaires.




Ajouter un commentaire
Veuillez vous connecter pour ajouter un commentaire.