Algorithmes de tris
- Les algorithmes de tri, sont utilisés principalement pour les tableaux (et les listes), ils peuvent aller du plus simple au plus compliquer.
- Donnée : Un tableau de n éléments (a0,a1, . . . ,an-1)
- Résultat : Une permutation (a’0,a’1, . . . ,a’n-1) du tableau d’entrée telle
a’0≤a’1 ≤ . . . ≤ a’n-1 ou a’0≥a’1 ≥ . . . ≥ a’n-1
- L’opération de base pour les algorithmes de tri est la comparaison : A[i] : A[j],
- Une autre opération est l’échange : on peut échanger A[i] et A[j], ce que l’on note par A[i] « A[j]. Le résultat est alors le suivant :
k ¬ A[i]
A[i] ¬ A[j] A[j] ¬ k
Le tri à bulle
- C’est un des algorithmes le plus connu moins efficace mais correcte.
- Le principe consiste à balayer tout le tableau, en comparant les éléments adjacents et en les échangeant s’ils ne sont pas dans le bon ordre. Ce processus est répété à chaque fin de tableau jusqu’à aucun échange ne sera effectué.
- Ce tri va nécessiter un grand nombre de déplacements d’éléments, il est donc inutilisable dans les cas où ces déplacements sont coûteux en temps.
- Il peut être intéressant quand le tableau initial est pré-trié (classement alphabétique)
Algorithme : TRI-BULLE
Données : A: tableau [0..n-1] : entier Variable : i, x : entier
Echange : booléen
début
Répéter
Echange Faux
pour i de 1 à n-2 faire
Si A[i-1]>A[i] alors
Echange Vrai x A[j]
A[j] A[i] A[i] x
finSi jusqu’à non Echange
fin
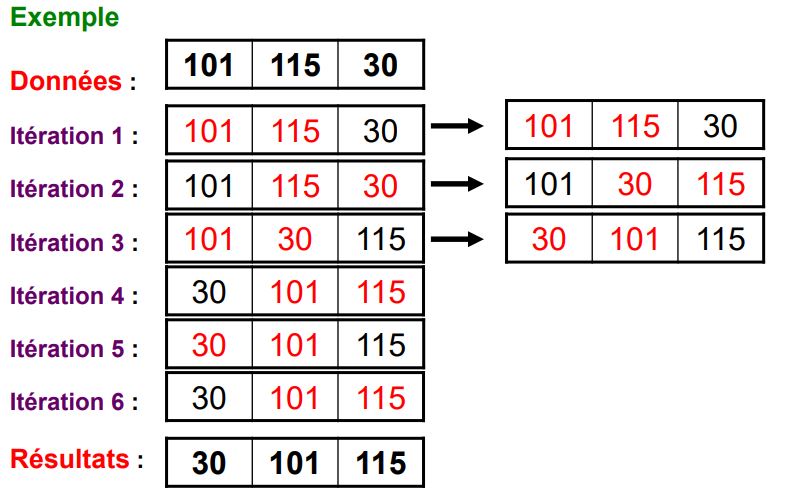
Le tri par insertion
- Prendre les éléments du tableau l’un après l’autre dans l’ordre initial, et les placer correctement dans les éléments précédents déjà triés (classement des cartes de jeux après une donne).
- A l’itération k, le kème élément est inséré d’une manière séquentielle parmi les premiers (k − 1) éléments qui sont déjà triés, cet l’opération est répété n fois (n taille du tableau)
- Le tri par insertion peut être intéressant pour des tableaux ayant déjà été
triés, mais où l’on doit rajouter quelques nouveaux éléments.
- Complexité : le nombre de comparaison à l’itération k est au plus k, le nombre total de comparaison est au plus (n(n+1)/2)-1 Î Q(n2)
Algorithme : TRI-INSERTION Données : A: tableau [0..n-1] : entier Variable : i, x, k : entier
début
pour i de 1 à n-1 faire
ki-1
x A[i]
Tant que A[k]>x faire
A[k+1] A[k]
k k-1
finTq
A[k+1] x
finPour
fin
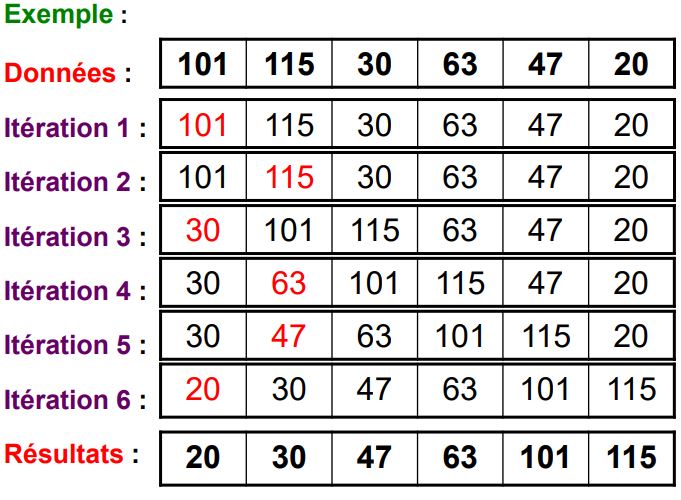
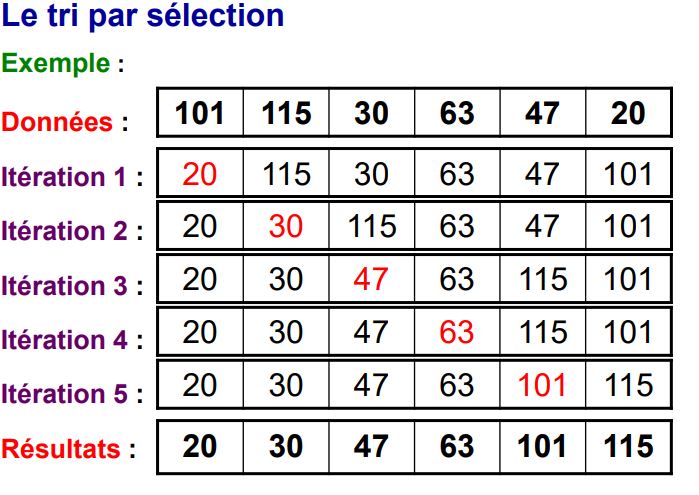
Le tri par sélection
- Le but est désormais de déplacer chaque élément à sa position définitive.
- Rechercher de l’élément le plus petit (ou plus grand) et l’échanger avec l’élément de la première position de la liste de recherche, l’opération est répétée n-1 fois
- Après le kème placement, les k plus petits éléments du tableau sont à leur place définitive, il faut recommencer avec la liste des éléments restants du tableau
- Complexité : le nombre de comparaison à l’itération k est n-k, le nombre total de comparaison est n(n-1)/2 Î Q(n2)
Algorithme : TRI-INSERTION Données : A: tableau [0..n-1] : entier Variable : i, x, k,j : entier
Début
i0
Tant que i<n-1 faire { ième placement } ji
pour k de i+1 à n-1 faire
Si A[k]<A[j] faire
j k
finPour
x A[j] A[j] A[i]
A[i] x
finTq
fin
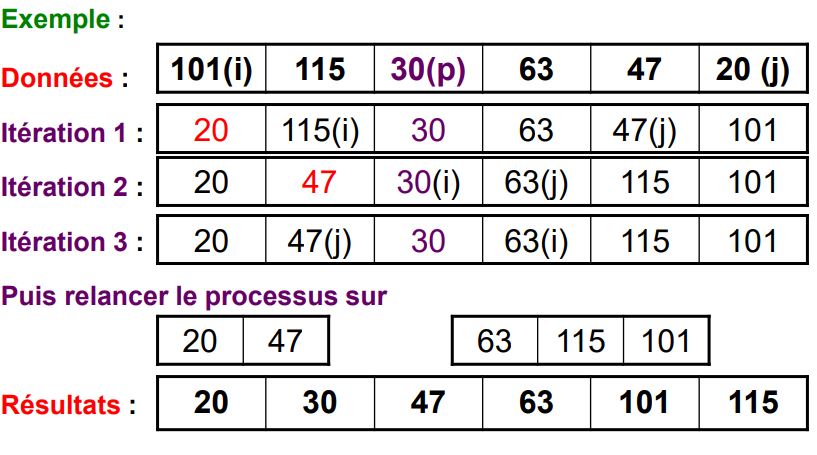
Le tri rapide (Quick Sort)
- Ce tri est récursif. On cherche à trier une partie du tableau, délimitée par les indices gauche et droite.
- Un pivot est choisi aléatoirement parmi les valeurs du tableau
- Recherche de la position définitive de ce pivot de telle sorte que tous les éléments avant le pivot soient plus petit que lui et que tous ceux placés après lui soient supérieurs (mais sans chercher à les classer)
- Rappelle récursif du tri de la partie avant le pivot et de la partie après le pivot jusqu’à que les parties ne contiennent qu’un seul élément
- Complexité en pire cas : Q(n2) et en meilleur cas : Q(n× log(n))
Algorithme : TRI-RAPIDE
Données : A: tableau [0..n-1] , gch, drt : entier Variable : i, j, x, pivot : entier
début
i gch j drt pivot A[(i+j)/2]
répéter
tant que t[i]<pivot faire
i i+1
tant que t[j]> pivot faire
j j-1
si i<= j alors
echanger(A[i],A[j]) i i+1
j j-1
finsi
jusqu'à ce que i>j
Algorithme : TRI-RAPIDE
Données : A: tableau [0..n-1] , gch, drt : entier Variable : i, j, x, pivot : entier
Début (suite)
si gch < j alors
Tri-Rapide(A,gch,j)
finsi
si i < drt alors
Tri-Rapide(A,i,droit)
finsi
fin
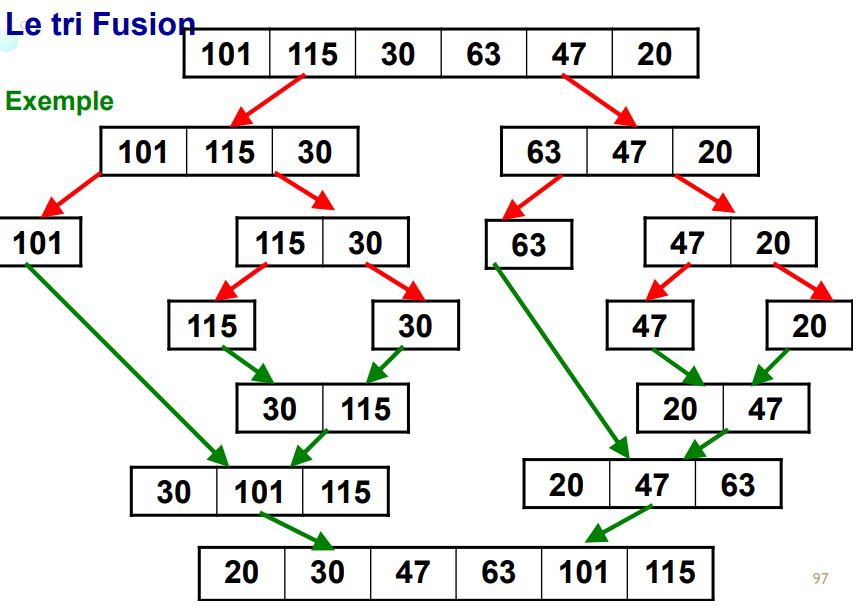
Le tri Fusion (mergesort)
- Application de la méthode diviser pour régner au problème du tri d’un tableau
- Le principe est de diviser une table de longueur n en deux tables de longueur n/2, de trier récursivement ces deux tables, puis de fusionner les tables triées.
- Complexité en pire cas : Q(n2) et en meilleur cas : Q(n× log(n))
Le tri Fusion (mergesort)
Première phase : Découpe :
- Découper le tableau en 2 sous-tableaux égaux (à 1 case près)
- Découper chaque sous-tableau en 2 sous-tableaux égaux
- Ainsi de suite, jusqu’à obtenir des sous-tableaux de taille 1
Deuxième phase : Tri/fusion :
- Fusionner les sous-tableaux 2 à 2 de façon à obtenir des sous- tableaux de taille 2 triés
- Fusionner les sous-tableaux 2 à 2 de façon à obtenir des sous-tableaux de taille 4 triés
- Ainsi de suite, jusqu’à obtenir le tableau entier
Le tri Fusion (mergesort)
Algorithme : FUSION
Données : A: tableau [0..n-1] , a, b,c : entier Variable : i,j,k : entier
A1 : tableau[0…b-a] , A2 :tableau [0…c-b-1] :entier
début
pour i de 0 à b-a faire
A1[i]<-- A[a+i]
pour j de 0 à c-b-1 faire
A2[j] <-- A[b+1+j]
i <-- 0
j <-- 0 k <-- a
Algorithme : FUSION(suite)
tant que (k <= c) faire
si (i >= b-a) alors
A[k] <-- A2[j] j <-- j+1
sinon
si (j >= c-b-1) alors
A[k] <-- A1[i] i <-- i+1
sinon
si (A1[i] <= A2[j]) alors
A[k] <-- A1[i] i <-- i+1
sinon
A[k] <-- A2[j] j <-- j+1
finsi
finsi
finsi
finsi
k++
fintantque
fin
Le tri Fusion (mergesort)
Algorithme : TRI-FUSION
Données : A: tableau [0..n-1] , a, b : entier début
si (b>a) alors
triFusion(A,a,(a+b)/2) triFusion(A,((a+b)/2)+1,b)
fusion(A,a,(a+b)/2,b)
finsi
fin
La recherche séquentielle
- A partir d’un tableau trié, on parcours ce tableau élément par élément
jusqu’à trouver le bon élément.
La recherche dichotomique
- La recherche dichotomique recherche un élément dans un tableau trié et retourne l’indice d’une occurrence de cet élément.
- Le principe consiste à compare l’élément cherché à celui qui se trouve au milieu du tableau. Si l’élément cherché est plus petit, alors continuer la recherche dans la première moitié du tableau, sinon dans la seconde moitié.
- Recommencer ce processus sur la moitié et s’arrêter lorsque l’on a
trouvé l’élément, ou lorsque l’intervalle de recherche est nul.
Pas encore de commentaires.



Ajouter un commentaire
Veuillez vous connecter pour ajouter un commentaire.