Modèle Conceptuel des Données au Modèle Logique des Données

1.   Introduction.................................................................................................

1.1.  Transformation d’un individu ou entité type.......................................

1.2.  Transformation d’une relation binaire (0,n)-(1,1) ou (1,n)-(1,1)..........

1.3.  Transformation d’une relation binaire (0,n)-(0,1) ou (1,n)-(0,1)..........

1.4.  Transformation d’une relation binaire (0,1)-(1,1).................................

1.5.  Transformation d’une relation binaire (0,1)-(0,1).................................

1.6.  Transformation d’une relation binaire (*,n)-(*,n).................................

1.7.  Transformation d’une relation ternaire et supérieure quelles que soit les cardinalités......................................................................................................

1. Introduction

Nous allons étudier dans ce document comment effectuer la transformation du Modèle Conceptuel des Données au Modèle Logique des Données. 

Le modèle logique sera la représentation du modèle physique qui sera implémenté sur le Système de Gestion de Bases de Données retenu. La modélisation logique ne prend pas en considération les spécificités du langage de définition de données relatif à l’outil informatique.

Toutefois, le modèle logique tient compte du type de SGBD. Il en existe deux types :

• Le modèle logique de données relationnel. Défini par CODD en 1970. De très loin le plus utilisé aujourd’hui compte tenu de la domination des SGBD relationnels.
• Le modèle logique de données navigationnel qui suit les recommandations CODASYL. Ces normes sont décrites sous la norme COBOL CODASYL. 

Nous nous intéresserons uniquement au modèle logique de données relationnel. Les bases de données conformes à Codasyl sont aujourd’hui peu usitées en dehors de l’utilisation sur certains systèmes Mainframe bien que la plupart aient migrés vers le relationnel.

1.1 Transformation d’un individu ou entité type

Tout individu devient une table. Ses propriétés deviennent des attributs de la table (colonne). L’identifiant devient la clé primaire unique de la table.*

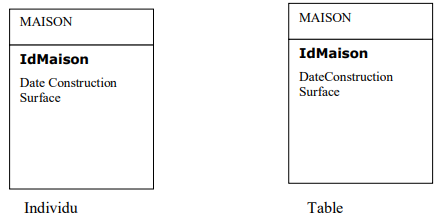
1.2 Transformation d’une relation binaire (0,n)-(1,1) ou (1,n)(1,1)

On duplique la clé issue de l’identifiant de l’individu porteur de la cardinalité (0,n) ou (1,n) dans la table issue de l’individu à cardinalité (1,1).Celle-ci devient alors une clé étrangère.

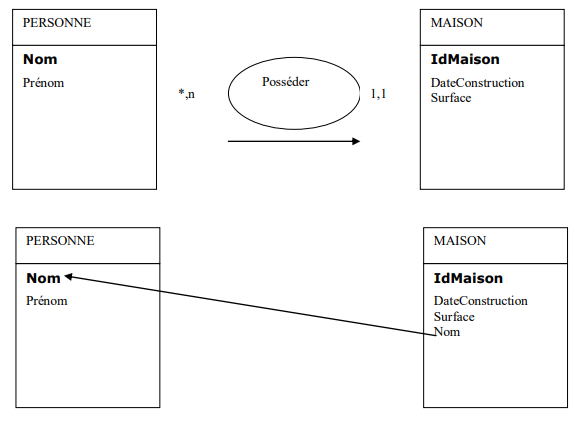
Il est nécessaire de se poser la question de la qualité de l’identifiant de la table personne. Dans la réalité, et conformément aux règles de normalisation, il serait préférable de mettre un identifiant qui soit stable. Dans l’exemple prit, il s’agit d’un principe de simplification ….

En France une femme qui se marie prend en général le nom de son mari : elle aura ainsi deux noms, le nom de jeune fille et le nom marital, une règle qui n’est toutefois pas vraie pour le Maroc. Le domaine d’études dans notre exemple n’est pas défini, mais il est probable que l’homonymie puisse se rencontrer dans notre système d’information.

1.3 Transformation d’une relation binaire (0,n)-(0,1) ou (1,n)(0,1)

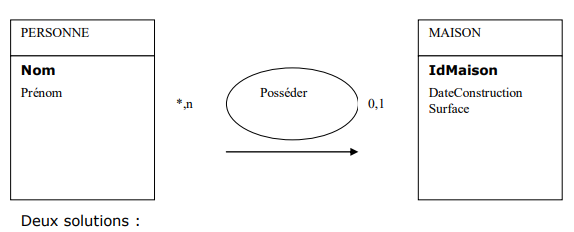
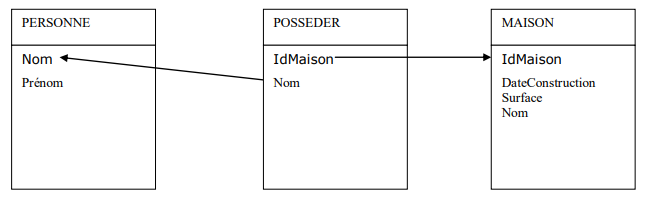
• Création d’une table avec comme clé primaire l’identifiant de l’individu porteur de la cardinalité (0,1) et comme clé étrangère l’identifiant de l’individu porteur de la cardinalité (*,n).
• Duplication de l’identifiant de l’individu porteur de la cardinalité (*,n) dans la table issue de l’individu porteur de la cardinalité (0,1) qui devient alors une clé étrangère. Il faut pour cette deuxième solution que le SGBD cible accepte des valeurs nulles pour la clé étrangère.

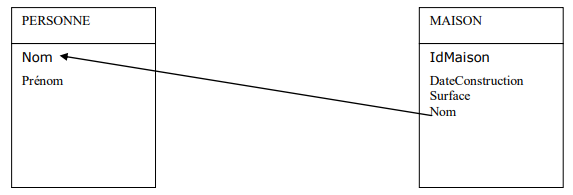
1.4 Transformation d’une relation binaire (0,1)-(1,1) 

La clé issue de l’identifiant de l’entité porteuse de la cardinalité (0,1) est dupliquée dans la table issue de l’entité porteuse de la cardinalité (1,1) et devient une clé étrangère.

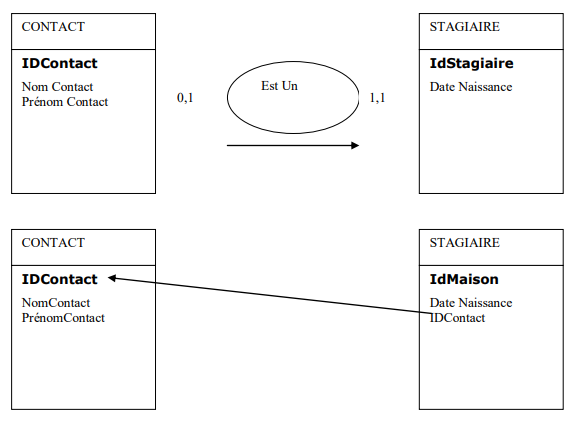
1.5 Transformation d’une relation binaire (0,1)-(0,1) 

C’est une particularisation des cas précédemment traités. 2 types de solutions sont possibles qui peuvent donner lieu à quatre solutions au final

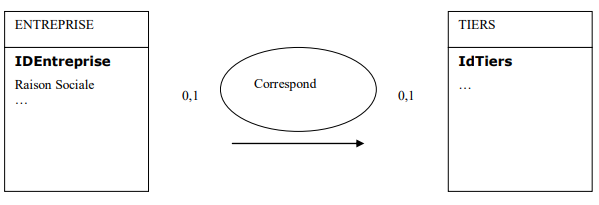
1. type de solution : Créer une table avec comme attributs les identifiants des individus en relation et comme clé primaire l’un des identifiants d’une des deux tables. Les deux attributs sont des clés étrangères. Exemple de schémas relationnels :

   Table ENTREPRISE(IDEntreprise, RaisonSociale,…)

   Table TIERS (IdTiers,…)

   Table CORRESPOND (Idtiers, IDEntreprise) 

    

2. type de solution : Duplication de la clé d’une des deux tables issues des entités types dans l’autre table.

Table ENTREPRISE (IDEntreprise,RaisonSociale,…,IDtiers)

Table TIERS (IdTiers,…)

Ou

Table ENTREPRISE (IDEntreprise,RaisonSociale,…)

Table TIERS (IdTiers,…,IDEntreprise)

1.6 Transformation d’une relation binaire (*,n)-(*,n) 

1. La solution consiste à créer une table dont la clé sera une clé composée des identifiants des deux entités en relation. Les propriétés éventuelles de la relation seront des attributs de la table.

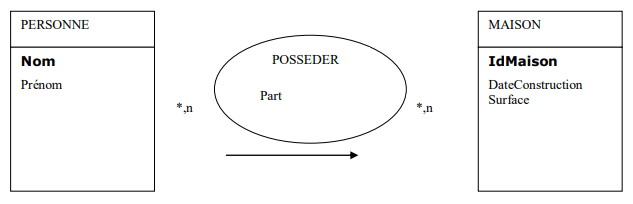
La table POSSEDER aura comme schéma relationnel POSSEDER (Nom, IDMaison, Part)

1.7 Transformation d’une relation ternaire et supérieure quelles que soit les cardinalités

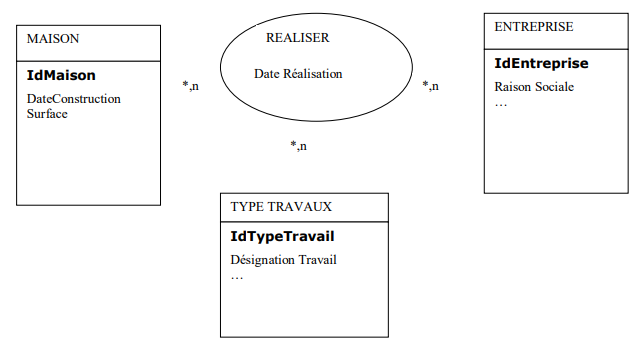
La relation donne lieu à la création d’une table qui aura comme clé primaire une clé composée des identifiants des individus sur lesquels portent la relation.  La table REALISER aura comme schéma relationnel 

REALISER (IdEntreprise, IDMaison, IdTypeTravail, DateRealisation)